Приветствую всех, дорогие друзья!
Ну что, поздравляю! Мы с вами благополучно добрались до основного материала в интегрировании рациональных дробей - метода неопределённых коэффициентов . Великого и могучего.) В чём же заключается его величество и могущество? А заключается оно в его универсальности. Имеет смысл ознакомиться, правда? Предупреждаю, что уроков по данной теме будет несколько. Ибо тема очень длинная, а материал крайне важный.)
Сразу скажу, что в сегодняшнем уроке (и последующих тоже) мы будем заниматься не столько интегрированием, сколько… решением систем линейных уравнений! Да-да! Так что те у кого проблемы с системами, повторите матрицы, определители и метод Крамера. А тех товарищей, у кого и с матрицами туго, призываю, на худой конец, освежить в памяти хотя бы "школьные" методы решения систем - метод подстановки и метод почленного сложения/вычитания.
Для начала нашего знакомства отмотаем плёнку немного назад. Ненадолго вернёмся к прошлым урокам и проанализируем все те дроби, которые мы с вами интегрировали до этого. Напрямую, безо всякого метода неопределённых коэффициентов! Вот они, эти дроби. Я рассортировал их по трём группам.
Группа 1
В знаменателе – линейная функция либо сама по себе, либо же в степени . Одним словом, в знаменателе стоит произведение одинаковых скобок вида (х-а) .
Например:
(x+4) 1 = (x+4)
(x-10) 2 = (x-10)(x-10)
(2x+5) 3 = (2x+5)(2x+5)(2x+5)
И так далее. Кстати, пусть вас не смущают скобки (4х+5) или (2х+5) 3 с коэффициентом k внутри. Это всё равно, по своей сути, скобки вида (х-а) . Ибо это самое k из таких скобок всегда можно вынести наружу.
Вот так:

Вот и всё.) И неважно, что именно при этом стоит в числителе – просто dx или же многочлен какой. Мы всегда раскладывали числитель по степеням скобки (x-a) , превращали большую дробь в сумму маленьких, подводили (где надо) скобку под дифференциал и интегрировали.
Группа 2
Что общего у этих дробей?
А общее то, что во всех знаменателях стоит квадратный трёхчлен ax 2 + bx + c . Но не просто, а именно в единственном экземпляре . И неважно здесь, положительный у него дискриминант или отрицательный.
Такие дроби всегда интегрировались одним из двух способов - либо разложением числителя по степеням знаменателя, либо выделением полного квадрата в знаменателе с последующей заменой переменной. Всё зависит от конкретной подынтегральной функции.
Группа 3
Это были самые нехорошие для интегрирования дроби. В знаменателе – неразложимый квадратный трёхчлен, да ещё и в степени n . Но, опять же, в единственном экземпляре . Ибо, кроме трёхчлена, других множителей в знаменателе нету. Такие дроби интегрировались по . Либо напрямую, либо сводились к ней после выделения полного квадрата в знаменателе и последующей замены переменной.
Однако, к сожалению, всё богатое многообразие рациональных дробей не ограничивается только лишь этими тремя рассмотренными группами.
А как быть, если в знаменателе стоят разные скобки? Например, что-нибудь типа:
(х-1)(х+1)(х+2)
Или одновременно скобка (х-а) и квадратный трёхчлен, что-то типа (х-10)(х 2 -2х+17) ? И в других подобных случаях? Вот, именно в таких случаях и приходит на помощь метод неопределённых коэффициентов !
Сразу скажу: работать мы пока что будем только с правильными дробями. Теми, у которых степень числителя строго меньше степени знаменателя. Как быть с неправильными дробями, подробно рассказано в по дробям. Надо выделять целую часть (многочлен). Делением уголком числителя на знаменатель или разложением числителя – как хотите. И даже пример разобран. А многочлен вы уж как-нибудь худо-бедно проинтегрируете. Не маленькие уже поди.) Но на неправильные дроби тоже порешаем примеры!
А теперь начинаем знакомиться. В отличие от большинства учебников по высшей математике, наше знакомство мы начнём не с сухой и грузной теории про основную теорему алгебры, теорему Безу, про разложение рациональной дроби на сумму простейших (об этих дробях позже) и прочего занудства, а начнём мы с несложного примера.
Например, нам требуется найти вот такой неопределённый интеграл:

Первый взгляд на подынтегральную дробь. В знаменателе стоит произведение трёх скобок:
(x-1)(x+3)(x+5)
Причём все скобки разные . Поэтому наша старая технология с разложением числителя по степеням знаменателя в этот раз уже не прокатывает: какую именно скобку выделять в числителе? (х-1)? (х+3)? Непонятно… Выделение полного квадрата в знаменателе – тоже не в кассу: там многочлен третьей степени (если перемножить все скобки). Что делать?
При взгляде на нашу дробь возникает вполне естественное желание… Прямо-таки непреодолимое! Из нашей большой дроби, которую неудобно интегрировать, как-то сделать три маленьких. Хотя бы вот так:
Почему именно такой вид надо искать? А всё потому, что в таком виде наша исходная дробь уже удобна для интегрирования! Подводим знаменатель каждой маленькой дроби и – вперёд.)
А можно ли вообще получить такое разложение? Новость хорошая! Соответствующая теорема математики гласит – да, можно ! Такое разложение существует и единственно.
Но есть одна проблемка: коэффициенты А , В и С мы пока не знаем. И сейчас нашей основной задачей как раз и будет их определить . Узнать, чему же равны наши буковки А , В и С . Отсюда и название – метод неопределённых коэффициентов. Начнём наше сказочное путешествие!
Итак, у нас есть равенство, от которого мы начинаем плясать:
Давайте приведём справа все три дроби к общему знаменателю и сложим:
Теперь можно смело отбросить знаменатели (ибо они одинаковы) и просто приравнять числители. Всё как в обычном
Следующим шагом раскрываем все скобки (коэффициенты А , В и С пока лучше оставить снаружи):
А теперь (важно!) выстраиваем всю нашу конструкцию справа по старшинству степеней : сначала собираем в кучку все члены с х 2 , потом - просто с иксом и, наконец, собираем свободные члены. Фактически, просто приводим подобные и группируем слагаемые по степеням икс.
Вот так:
А теперь осмысливаем результат. Слева - наш исходный многочлен. Второй степени. Числитель нашей подынтегральной дроби. Справа - тоже некоторый многочлен второй степени. Но с неизвестными коэффициентами. Данное равенство должно быть справедливо при всех допустимых значениях икс . Дроби-то слева и справа были одинаковые (по нашему условию)! Это означает, что их числител и (т.е. наши многочлены) - тоже одинаковые. Стало быть, коэффициенты при одинаковых степенях икс у этих многочленов обязательно должны быть равны!
Начинаем с самой старшей степени. С квадрата. Смотрим, что за коэффициенты у нас стоят при х 2 слева и справа. Справа у нас стоит сумма коэффициентов А+В+С , а слева – двойка. Так у нас рождается первое уравнение.
Записываем:
А+В+С = 2
Есть. Первое уравнение готово.)
Далее идём по снижающейся траектории – смотрим на члены с иксом в первой степени. Справа при икс у нас стоит 8А+4В+2С . Хорошо. А что у нас при икс стоит слева? Гм… Слева вообще никакого слагаемого с иксом нету! Там только 2х 2 - 3. Как быть? Очень просто! Это значит, что коэффициент при икс слева у нас равен нулю! Мы же можем записать нашу левую часть вот так:
![]()
А что? Имеем полное право.) Отсюда второе уравнение выглядит так:
8 A +4 B +2 C = 0
Ну вот, практически, и всё. Осталось приравнять свободные члены:
15А-5В-3С = -3
Одним словом, приравнивание коэффициентов при одинаковых степенях икса происходит по такой схеме:

Все три наших равенства должны выполняться одновременно. Поэтому собираем из наших выписанных уравнений систему:

Системка не самая трудная для прилежного студента – три уравнения и три неизвестных. Как хотите, так и решайте. Можно методом Крамера через матрицы с определителями, можно методом Гаусса, можно даже обычной школьной подстановкой.
Для начала я решу эту систему так, как обычно решают такие системы культурные студенты. А именно - методом Крамера.
Решение начинаем с составления матрицы системы. Напоминаю, что эта матрица - просто табличка, составленная из коэффициентов при неизвестных.
Вот она:

Первым делом вычисляем определитель матрицы системы. Или, коротко, определитель системы. Обычно он обозначается греческой буквой ∆ ("дельта"):
Отлично, определитель системы не равен нулю (-48 ≠0) . Из теории систем линейных уравнений этот факт означает, что наша система совместна и имеет единственное решение.
Следующим шагом вычисляем определители неизвестных ∆ A , ∆ B , ∆ C . Напоминаю, что каждый из этих трёх определителей получается из основного определителя системы путём замены столбцов с коэффициентами при соответствующих неизвестных на столбец свободных членов.
Вот и составляем определители и считаем:
Подробно объяснять технику вычисления определителей третьего порядка я здесь не буду. И не просите. Это уже совсем отклонение от темы будет.) Кто в теме, тот понимает, о чём речь. И, возможно, уже догадался, каким именно способом я вычислил эти три определителя.)

Вот всё и готово.)
Так обычно решают системы культурные студенты. Но… Не все студенты дружат с и определителями. К сожалению. Для кого-то эти простые понятия высшей математики так навсегда и остаются китайской грамотой и таинственным монстром в тумане...
Что ж, специально для таких некультурных студентов предлагаю более привычный способ решения - метод последовательного исключения неизвестных. Фактически, это продвинутый "школьный" метод подстановки. Только шагов побольше будет.) Но суть та же самая. Первым делом я исключу переменную С . Для этого я выражу С из первого уравнения и подставлю во второе и третье:
Упрощаем, приводим подобные и получаем новую систему, уже с двумя неизвестными:
Теперь, в этой новой системе, тоже можно выразить одну из переменных через другую. Но самые внимательные студенты, возможно, заметят, что коэффициенты перед переменной B – противоположны . Два и минус два. Стало быть, очень удобно будет сложить между собой оба уравнения, чтобы исключить переменную В и оставить только букву А .
Складываем левые и правые части, мысленно сокращаем 2B и -2B и решаем уравнение только относительно А :
Есть. Первый коэффициент найден: А = -1/24 .
Определяем второй коэффициент В . Например, из верхнего уравнения:
Отсюда получаем:

Отлично. Второй коэффициент тоже найден: B = -15/8 . Осталась ещё буковка С . Для её определения используем самое верхнее уравнение, где она у нас выражена через А и В :
Итак:
Ну вот и всё. Неизвестные коэффициенты найдены! Неважно, через Крамера или через подстановку. Главное, правильно найдены.)
Стало быть, наше разложение большой дроби в сумму маленьких будет выглядеть вот так:
И пусть вас не смущают полученные дробные коэффициенты: в данной процедуре (методе неопределённых коэффициентов) это самое обычное явление. :)
А теперь крайне желательно проверить, правильно ли мы нашли наши коэффициенты A , B и С . Поэтому сейчас берём черновик и вспоминаем восьмой класс – складываем обратно все три наши маленькие дроби.
Если мы получим исходную большую дробь – значит, всё хорошо. Нет – значит, бейте меня ищите ошибку.
Общий знаменатель, очевидно, будет 24(х-1)(х+3)(х+5).
Поехали:

Йес!!! Получили исходную дробь. Что и требовалось проверить. Всё гуд. Так что прошу не бить.)
А теперь возвращаемся к нашему исходному интегралу. Легче он за это время не стал, да. Но теперь, когда наша дробь разложена в сумму маленьких, её интегрирование стало сплошным удовольствием!
Смотрите сами! Вставляем наше разложение в исходный интеграл.
Получаем:
Пользуемся свойствами линейности и разбиваем наш большой интеграл в сумму маленьких, все константы выносим за знаки интеграла.
Получаем:
А полученные три маленьких интеграла уже легко берутся .
Продолжаем интегрирование:
Вот и всё.) И не надо в данном уроке спрашивать меня, откуда в ответе взялись логарифмы! Кто помнит , тот в теме и всё поймёт. А кто не помнит - гуляем по ссылочкам. Я их не просто так ставлю.
Окончательный ответ:
Вот такая красивая троица: три логарифма – трус, бывалый и балбес. :) И попробуй, догадайся до такого хитрого ответа с ходу! Только метод неопределённых коэффициентов и выручает, да.) Собственно, с этой целью и разбираемся. Что, как и откуда.
В качестве тренировочного упражнения, предлагаю вам попрактиковаться в методе и проинтегрировать вот такую дробь:

Потренируйтесь, найдите интеграл, не сочтите за труд! Должен получиться вот такой ответ:
Метод неопределённых коэффициентов – штука мощная. Спасает даже в самой безнадёжной ситуации, когда и так дробь преобразовываешь, и эдак. И вот тут у некоторых внимательных и интересующихся читателей, возможно, возник целый ряд вопросов:
- Что делать, если многочлен в знаменателе вообще не разложен на множители?
- КАК надо искать разложение любой большой рациональной дроби на сумму маленьких? В каком виде? Почему именно в таком, а не сяком?
- Что делать, если в разложении знаменателя есть кратные множители? Или скобки в степенях типа (х-1) 2 ? В каком виде искать разложение?
- Что делать, если, помимо простых скобок вида (х-а), знаменатель одновременно содержит и неразложимый квадратный трёхчлен? Скажем, х 2 +4х+5 ? В каком виде искать разложение?
Что ж, пришла пора основательно разбираться, откуда ноги растут. В следующих уроках.)
Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений , а также на их комбинации.
Простейшие дроби часто называют элементарыми дробями .
Различают следующие виды простейших дробей :
где A , M , N , a , p , q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля.
Называют их соответственно дробями первого, второго, третьего и четвертого типов.
Для чего вообще дробь раскладывать на простейшие?
Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов.
К примеру, требуетя взять интеграл от дробно рациональной функции
. После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам
Но об интегралах в другом разделе.
Пример.
Разложить дробь на простейшие.
Решение.
Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя , а уже затем проводят разложение правильной дробно рациональной функции.
Выполним деление столбиком (уголком):
Следовательно, исходная дробь примет вид:
Таким образом, на простейшие дроби будем раскладывать
Алгоритм метода неопределенных коэффициентов.
Во-первых , раскладываем знаменатель на множители.
В нашем примере все просто – выносим х
за скобки.![]()
Во-вторых , раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами .
Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.
Хватит теории, на практике все равно понятнее.
Пришло время вернуться к примеру. Дробь раскладывается в сумму простейших дробей первого и третьего типов с неопределенными коэффициентами A
, B
и C
.![]()
В-третьих
, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х
.
То есть, пришли к равенству:
При x
отличных от нуля это равенство сводится к равенству двух многочленов
А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.
В-четвертых , приравниваем коэффициенты при одинаковых степенях х .
При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:
В-пятых
, решаем полученную систему уравнений любым способом (при необходимости смотрите статью ), который нравится Вам, находим неопределенные коэффициенты.
В-шестых
, записываем ответ.
Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение.
Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие.
Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с
Рассмотрим на примере, чтобы показать плюсы этого метода.
Пример.
Разложить дробь ![]() на простейшие.
на простейшие.
Решение.
Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то производить деление нам не придется. Переходим к разложению знаменателя на множители.
Для начала выносим х
за скобки.
Находим корни квадратного трехчлена (например, по теореме Виета):
Следовательно, квадратный трехчлен можно записать как
То есть, знаменатель примет вид
При данном знаменателе, исходная дробь раскладывается в сумму трех простейших дробей первого типа с неопределенными коэффициентами:
Полученную сумму приводим к общему знаменателю, но в числителе при этом скобки не раскрываем и не приводим подобные при А
, В
и С
(на этом этапе как раз отличие от метода неопределенных коэффициентов):
Таким образом, пришли к равенству:
А теперь, для нахождения неопределенных коэффициентов, начинаем подставлять в полученное равенство «частные значения», при которых знаменатель обращается в ноль, то есть х=0 , х=2 и х=3 для нашего примера.
При х=0
имеем:
При х=2
имеем:
При х=3
имеем:
Ответ:
Как видите, различие метода неопределенных коэффициентов и метода частных значений лишь в способе нахождения неизвестных. Эти методы можно совмещать для упрощения вычислений.
Рассмотрим пример.
Пример.
Разложить дробно рациональное выражение  на простейшие дроби.
на простейшие дроби.
Решение.
Так как степень многочлена числителя меньше степени многочлена знаменателя и знаменатель уже разложен на множители, то исходное выражение представится в виде суммы простейших дробей следующего вида:
Приводим к общему знаменателю:
Приравниваем числители.
Очевидно, что нулями знаменателя являются значения х=1 , х=-1 и х=3 . Используем метод частных значений.
При х=1
имеем:![]()
При х=-1
имеем:![]()
При х=3
имеем:![]()
Осталось найти неизвестные и
Для этого подставляем найденные значения в равенство числителей:
После раскрытия скобок и приведения подобных слагаемых при одинаковых степенях х приходим к равенству двух многочленов:
Приравниваем соответствующие коэффициенты при одинаковых степенях, тем самым составляем систему уравнений для нахождения оставшихся неизвестных и . Получаем систему из пяти уравнений с двумя неизвестными:
Из первого уравнения сразу находим , из второго уравнения
В итоге получаем разложение на простейшие дроби:
Примечание.
Если бы мы сразу решили применить метод неопределенных коэффициентов, то пришлось бы решать систему пяти линейных алгебраических уравнений с пятью неизвестными. Применение метода частных значений позволило легко отыскать значения трех неизвестных из пяти, что значительно упростило дальнейшее решение.
Метод применим для минимизации функций алгебры логики от любого числа переменных.
Рассмотрим случай трех переменных. Булева функция в ДНФ может быть представлена в виде всевозможных конъюнктивных членов, которые могут входить в ДНФ:
где kÎ{0,1} ‑ коэффициенты. Метод заключается в подборе коэффициентов таким образом, чтобы получаемая ДНФ была минимальной.
Если теперь задать всевозможные значения переменных от 000 до 111, то получим 2 n (2 3 =8) уравнений для определения коэффициентов k :
Рассматривая наборы, на которых функция принимает нулевое значение, определяют коэффициенты, которые равны 0, и вычеркивают их из уравнений, в правой части которых стоит 1. Из оставшихся коэффициентов в каждом уравнении к единице приравнивают по одному коэффициенту, определяющему конъюнкцию наименьшего ранга. Остальные коэффициенты приравнивают к 0. Итак, единичные коэффициенты k определяют соответствующую минимальную форму.
Пример . Минимизировать заданную функцию
если известны
значения:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.
Решение.
После вычеркивания нулевых коэффициентов получим:
 =1;
=1;
 =1;
=1;
 =1;
=1;
 =1.
=1.
Приравняем к
единице коэффициент
 ,
соответствующий конъюнкции наименьшего
ранга и обращающий четыре последних
уравнения в 1, а в первом уравнении
целесообразно приравнять к 1 коэффициент
,
соответствующий конъюнкции наименьшего
ранга и обращающий четыре последних
уравнения в 1, а в первом уравнении
целесообразно приравнять к 1 коэффициент .
Остальные коэффициенты приравнивают
к 0.
.
Остальные коэффициенты приравнивают
к 0.
Ответ : вид минимизированной функции .
Следует отметить, что метод неопределенных коэффициентов эффективен, когда число переменных невелико и не превышает 5-6.
Многомерный куб
Рассмотрим графическое представление функции в виде многомерного куба. Каждой вершине n -мерного куба можно поставить в соответствие конституенту единицы.

Подмножество отмеченных вершин является отображением на n -мерном кубе булевой функции от n переменных в СДНФ.
Для отображения функции от n переменных, представленной в любой ДНФ, необходимо установить соответствие между ее минитермами и элементами n -мерного куба.
Минитерм
(n-1)-го ранга
 можно рассматривать как результат
склеивания двух минитермовn
-го
ранга, т.е.
можно рассматривать как результат
склеивания двух минитермовn
-го
ранга, т.е.
 =
=

На n -мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координат х i , соединяющих эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины).
Таким образом, минитермам (n -1)-го порядка соответствуют ребра n-мерного куба.
Аналогично устанавливается соответствие минитермов (n -2)-го порядка граням n -мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы n -мерного куба, характеризующиеся S измерениями, называются S -кубами.
Так вершины являются 0-кубами, ребра 1-кубами, грани 2-кубами и т.д.
Обобщая, можно сказать, что минитерм (n-S ) ранга в ДНФ для функции n переменных отображается S -кубом, причем каждый S -куб покрывает все те кубы низшей размерности, которые связаны только с его вершинами.
Пример. На рис.
дано отображение


Здесь минитермы
 и
и соответствуют 1-кубам (S
=3-2=1),
а минитерм х
3
отображается 2-кубам (S
=3-1=2).
соответствуют 1-кубам (S
=3-2=1),
а минитерм х
3
отображается 2-кубам (S
=3-1=2).
Итак, любая ДНФ отображается на n -мерном кубе совокупностью S -кубов, которые покрывают все вершины, соответствующие конституентам единицам (0-куба).
Конституенты
.
Для переменных х
1
,
х
2
,…
х
n
выражение
 называют конституентой единицы, а
называют конституентой единицы, а - конституентой нуля (
- конституентой нуля ( означает либо
означает либо ,
либо
,
либо ).
).
Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания - нулю (единице).
Например:
конституенте единице
 соответствует набор (1011), а конституенте
нуля
соответствует набор (1011), а конституенте
нуля - набор (1001).
- набор (1001).
Так как СД(К)НФ является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f (x 1 , x 2 ,…, x n ) обращается в единицу (нуль) только при наборах значений переменных x 1 , x 2 ,…, x n , соответствующих этим копституантам. На остальных наборах эта функция обращается в 0 (единицу).
Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей.
Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам значений переменных, на которых функция принимает значение, равное единице (нулю).
Например, функции, заданной таблицей

соответствуют

Полученные выражения можно преобразовать к другому виду на основании свойств алгебры логики.
Справедливо и обратное утверждение: если некоторая совокупность S -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим S -кубам минитермов является выражением данной функции в ДНФ.
Говорят, что такая совокупность S -кубов (или соответствующих им минитермов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число S -кубов которого было бы поменьше, а их размерность S - побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием.
Например, для
функции у
= покрытие соответствует неминимальной
форме:
покрытие соответствует неминимальной
форме:
рис a) у =,
а покрытия на рис
б) у
= ,
рис в) у
=
,
рис в) у
= минимальные.
минимальные.

Рис. Покрытие функции у =:
а) неминимальное; б), в) минимальное.
Отображение функции
на n
-мерном
наглядно и просто при n
3.
Четырехмерный куб можно изобразить,
как показано на рис., где отображены
функции четырех переменных и ее
минимальное покрытие, соответствующее
выражению у
=

Использование этого метода при n >4 требует настолько сложных построений, что теряет все его преимущества.
Равенство (I) есть тождество. Приведя его к целому виду, получим равенство 2-х многочленов. Но такое равенство всегда выполняется лишь при условии почленного равенства этих многочленов.
Приравнивая коэффициенты при одинаковых степенях х, стоящих в левой и правой частях равенства, получим систему линейных уравнений относительно неизвестных коэффициентов, которую надлежит решить.
Так как разложение (I) всегда существует для любой правильной рациональной дроби, то полученная система всегда совместна.
Такой метод нахождения коэффициентов называется методом неопределенных коэффициентов (способ сравнения коэффициентов).
Приведем пример разложения рациональной функции на элементарные дроби.
Пример 6.6.27. Разложить дробь на элементарные.

последнее уравнение подставим во второе 
Таким образом,  .
.
x=2  ;
;
x=3  .
.
Следует; .
Метод частных значений требует меньших затрат труда и поэтому заслуживает особого внимания при интегрировании рациональных дробей.
Если корни знаменателя только действительные, то для определения неизвестных коэффициентов целесообразно пользоваться именно этим способом.
В остальных случаях для определения неизвестных коэффициентов можно комбинировать оба способа.
Замечание. Метод частных значений применяется и тогда, когда другие случаи, но здесь нужно тождество дифференцировать.
Таким образом, для интегрирования правильных рациональных дробей достаточно уметь:
1) интегрировать элементарные дроби;
2) разлагать рациональные дроби на элементарные.
3. Интегрирование рациональных дробей
Схема интегрирования рациональных дробей:
Для интегрирования рациональных дробей  ;
;
Где P(x) и Q(x) – многочлены с действительными коэффициентами, последовательно выполняют три шага.
Первый шаг. Если дробь неправильная, то есть степень числителя P(x) больше или равна степени знаменателя Q(x), выделяют целую часть рациональной дроби, деля числитель на знаменатель по правилу деления многочлена на многочлен. После этого рациональная дробь может быть записана в виде суммы:
1) выделенной целой части – многочлена М(х);
2) правильной остаточной дроби  :
:

Второй шаг.
Правильную остаточную дробь  разлагают на последующие дроби.
разлагают на последующие дроби.
Для этого находят корни уравнения Q(x)=0 и разлагают знаменатель Q(x) на множители первой и второй степени с действительными коэффициентами:
В этом разложении знаменателя множители 1-й степени соответствуют действительным корням, а множители 2-й степени – параллельных сопряженных корней.
Коэффициент при большей степени х в знаменателе Q(x) можно считать равным 1 ибо этого всегда можно добиться, делением на него P(x) и Q(x).
После этого правильная остаточная дробь разлагается на простейшие (элементарные).
Третий шаг. Находят интегралы выделенной целой части и всех элементарных дробей (методами, рассмотренными выше), которые затем складывают.
Пример6.6.28. 
Под знаком интеграла – неправильная рациональная дробь, так как степень числитель равна степени знаменателя, поэтому выделяем целую часть.
Рациональная функция - это дробь вида , числитель и знаменатель которой - многочлены или произведения многочленов.
Пример 1. Шаг 2.
 .
.
Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:
Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:
В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:
 .
.
Сокращаем все иксы и получаем эквивалентную систему уравнений:
 .
.
Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:
![]() .
.
Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
![]() .
.
Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:

Решаем полученную систему:

Итак, , отсюда
![]() .
.
Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
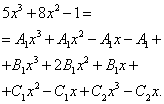
Как и в предыдущих примерах составляем систему уравнений:

Сокращаем иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
![]() .
.
Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
 .
.
Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
![]() .
.
Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
![]() .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
 .
.
Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
![]()
Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:
![]() .
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
![]() .
.
Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
 .
.
После известных действий с полученной суммой должна получиться следующая система уравнений:
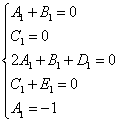
Решая систему, получаем следующие значения неопределённых коэффициентов:
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
 .
.
Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
 .
.
Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем.


